Модель Шварцшильда. Асимметричный дрейф

5.2 Модель Шварцшильда. Асимметричный дрейф

Средний радиус звезды, находящейся на почти круговой орбите вблизи экваториальной плоскости, в основном определяется угловым моментом $L_{z}$ (или радиусом $R_{g} (L_{z})$ ). Поэтому зависимость профиля плотности от радиуса в динамически «холодном» диске определяется, в основном, зависимостью ФР от $L_{z}$ . Разность

Δ \equiv H - E_{c} (L_{z})

(5.11)

между полной энергией звезды и энергией $E_{c} (L_{z})$ на круговой орбите с тем же угловым моментом – это энергия, связанная с движением по эпициклам (эллипсам). В диске, состоящем из большого количества звезд, эти осциллирующие движения складываются с разными фазами. Оно наложено на общее круговое движение. Таким образом создается дисперсия скоростей в каждой точке диска. Зависимость распределения от $Δ$ определяет дисперсию скоростей, или температуру, диска. В холодном диске все звезды имеют малые значения $Δ ∕ E_{c} (L_{z})$ . Используя эти соображения, сконструируем ФР в виде

f (H, L_{z}) = S (L_{z}) T [Δ ∕ σ^{2} (L_{z})],

(5.12)

где $S (L_{z})$ в основном определяется профилем поверхностной плотности $Σ (R)$ , функция $T$ – распределением скоростей, а $σ (L_{z})$ – профилем радиальной зависимости дисперсии скоростей.

ФР такого вида не могут быть использованы для описания солнечной окрестности, поскольку наблюдения дают $\bar{v_{z}^{2}} ∕ \bar{v_{R}^{2}} ≃ 0.3$ , тогда как согласно (1.65) отношение этих дисперсий должно быть единицей. Отсюда следует необходимость рассмотрения более сложных ФР, зависящих от третьего интеграла движения $I_{3}$ . Аналитического выражения для него в случае произвольного осесимметричного потенциала не существует, поэтому мы используем приближение:

I_{3} ≃ H_{z} (z, ż, L_{z}) = \frac{1}{2} ż^{2} + Φ_{z} (z, L_{z}),

(5.13)

где $Φ_{z} (R, z) = Φ (R, z) - Φ (R, 0)$ . Итак, мы пришли к ФР вида

f (H, L_{z}, I_{3}) = S (L_{z}) T (\frac{Δ}{σ_{R}^{2} (L_{z})}, \frac{I_{3}}{σ_{3}^{2} (L_{z})})

(5.14)

Естественный и простой выбор для $T (x, y) = exp (- x - y)$ . В эпициклическом приближении

Δ = H_{R} + H_{z}, H_{R} = \frac{1}{2} (ẋ^{2} + κ^{2} x^{2}),

(5.15)

поэтому получаем

f (H, L_{z}, I_{3}) = S (L_{z}) exp (- \frac{H_{R}}{σ_{R}^{2}} - \frac{H_{z}}{σ_{z}^{2}}), σ_{z}^{2} = \frac{σ_{R}^{2} σ_{3}^{2}}{σ_{R}^{2} + σ_{3}^{2}}

(5.16)

К сожалению, величина $R_{g}$ звезды – ненаблюдаема, поэтому нельзя определить $x$ . Однако, наблюдениям доступна скорость звезды относительно локального стандарта покоя (LSR), т.е. величина $\tilde{v} \equiv v - v_{c} (R) {\hat{e}}_{φ}$ . Используя эпициклическое приближение, имеем

\begin{align} {\tilde{v}}_{φ} = R (\dot{φ} - Ω (R)) ≃ R [(\dot{φ} - Ω_{g}) - (\frac{d Ω}{d R})_{R_{g}} x], & (5.17) \\ \dot{φ} - Ω_{g} \approx - Ω_{g} \frac{2 x}{R_{g}}, & (5.18) \end{align}

откуда

{\tilde{v}}_{φ} \approx - κ x ∕ γ

, что позволяет выписать функцию распределения в виде

f_{Sch} \equiv S (L_{z}) exp (- \frac{v_{R}^{2} + γ^{2} {\tilde{v}}_{φ}^{2}}{2 σ_{R}^{2} (L_{z})} - \frac{v_{z}^{2} + 2 Φ_{z} (z, L_{z})}{2 σ_{z}^{2} (L_{z})})

(5.19)

Эта ФР называется функцией распределения Шварцшильда.

Необходимо установить связь трех функций $S (L_{z}), σ_{R} (L_{z}), σ_{z} (L_{z})$ , определяющих распределение Шварцшильда, с наблюдаемыми величинами. Если эти функции меняются медленно, т.е. их производные порядка $σ^{'} \sim σ ∕ L_{z}$ , то

\frac{σ (L_{z}) - σ (R v_{c})}{σ (R v_{c})} \approx \frac{σ^{'}}{σ} R ṽ_{φ} \sim \frac{ṽ_{φ}}{v_{c}} ≪ 1,

(5.20)

поскольку для солнечной окрестности $v_{c} \approx 220$ км/с, а возмущенные азимутальные скорости даже самых старых звезд $σ_{R} (L_{z}) ≃ 40$ км/с. Поэтому с точностью до $ṽ_{φ} ∕ v_{c}$ величины $σ_{R} (R v_{c})$ и $σ_{z} (R v_{c})$ определяют дисперсии радиальной и вертикальной скоростей.

Для определения $S (L_{z})$ вычислим поверхностную плотность $Σ (R)$ . Интегрирование по скоростям дает объемную плотность:

ρ (R, z) = \int d^{3} v f ≃ {(2 π)}^{3 ∕ 2} S (R v_{c}) (\frac{σ_{R}^{2} σ_{z}}{γ})_{L_{z} = R v_{c}} exp (- \frac{Φ_{z} (z, R v_{c})}{σ_{z}^{2} (R v_{c})}) .

(5.21)

Если изменение потенциала $Φ_{z} (z, R v_{c})$ и зависимость плотности от $z$ самосогласованы (см. формулу (3.31) для изотермического слоя), а плотность имеет вид (5.21), то $Σ = 4 z_{0} ρ_{0}$ , где $z_{0} = σ_{z} {(8 π G ρ_{0})}^{- 1 ∕ 2}$ . Откуда получим связь между поверхностной плотностью и $S (L_{z})$ :

Σ (L_{z} ∕ v_{c}) ≃ Σ (R) ≃ 4 {(2 π)}^{3 ∕ 2} S (L_{z}) (\frac{σ_{R}^{2} σ_{z} z_{0}}{γ})_{L_{z}} .

(5.22)

Это выражение справедливо при $σ_{R} (L_{z}), σ_{z} (L_{z}) ≪ v_{c}$ .

Однако, мы можем использовать его для подстановки в (5.19), имея ввиду, что получающаяся из него поверхностная плотность не будет в точности равна $Σ (R)$ :

f_{Schw} \equiv \frac{γ Σ (L_{z} ∕ v_{c})}{4 {(2 π)}^{3 ∕ 2} σ_{R}^{2} σ_{z} z_{0}} exp (- \frac{v_{R}^{2} + γ^{2} ṽ_{φ}^{2}}{2 σ_{R}^{2} (L_{z})} - \frac{v_{z}^{2} + 2 Φ_{z} (z, L_{z})}{2 σ_{z}^{2} (L_{z})})

(5.23)

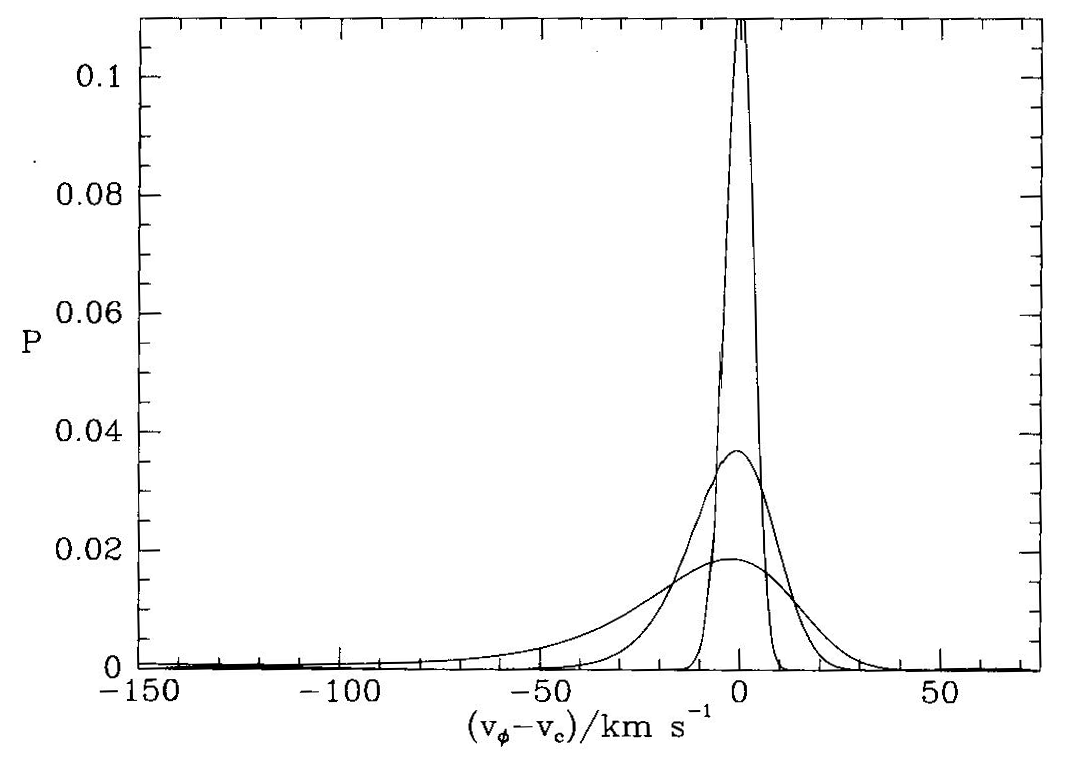
На Рис. 13 показаны различные варианты распределения Шварцшильда как функция от $ṽ_{φ} = v_{φ} - v_{c}$ . Видно, что есть асимметрия в распределении, которая является следствием зависимости поверхностной плотности и дисперсии скоростей от $L_{z}$ , а через нее – от $ṽ_{φ}$ .

Рис. 13: Три распределения возмущенной азимутальной скорости

ṽ_{φ}

, согласно (5.23), при плоской кривой вращения

v_{0} = 220

км/с,

σ_{R} (L_{z})

σ_{z} (L_{z})

приняты

\propto exp [- L_{z} ∕ (2 v_{0} R_{d})]

Σ = Σ_{0} exp (- R ∕ R_{d})

R_{0} ∕ R_{d} = 3.2

. Значения

σ_{R}

в окрестности Солнца приняты равными 5, 15 и 30 км/с.

Отклонение среднего значения $ṽ_{φ}$ от нуля называется асимметричным дрейфом и дается выражением Стромберга:

v_{a} = \frac{\bar{v_{R}^{2}}}{2 v_{c}} [\frac{σ_{φ}^{2}}{\bar{v_{R}^{2}}} - 1 - \frac{\partial ln (ν \bar{v_{R}^{2}})}{\partial ln R} - \frac{R}{\bar{v_{R}^{2}}} \frac{\partial (ν \bar{v_{R} v_{z}})}{\partial z}]

(5.24)

[next] [prev] [prev-tail] [front] [up]