Теоремы Джинса

1.4 Теоремы Джинса

Формулировки теорем Джинса следующие:

Любое стационарное решение бесстолкновительного уравнения Больцмана (1.23) зависит от фазовых переменных только через интегралы движения;
Любая функция интегралов движения является решением бесстолкновительного уравнения Больцмана.

Разберем, что такое интегралы движения, какие они бывают и чем отличаются от констант движения.

Константы движения

Константа движения – любая функция фазовых координат и времени, постоянная вдоль траектории частицы.

C [x (t_{1}), v (t_{1}); t_{1}] = C [x (t_{2}), v (t_{2}); t_{2}]

(1.47)

для любых $t_{1}$ и $t_{2}$ .

Пример: рассмотрим круговую орбиту в сферически–симметричном потенциале, где азимут

ψ = Ω t + ψ_{0}, C (ψ, t) = t - ψ ∕ Ω .

(1.48)

Выражение $C (ψ, t)$ является константой движения. Начальные условия ( $x_{0}, v_{0}$ ) также являются константами движения (всего 6 констант).

Интегралы движения

Интеграл движения – функция фазовых координат, постоянная вдоль траектории частицы

I [x (t_{1}), v (t_{1})] = I [x (t_{2}), v (t_{2})] .

(1.49)

Интеграл движения представляет собой частный случай константы движения.

Траектории могут иметь от 0 до 5 интегралов движения. Примеры интегралов движения:

H (x, v) = v^{2} ∕ 2 + Φ (x), L_{z} = x v_{y} - y v_{x}, L

(1.50)

Далее мы рассмотрим примеры, в которых интегралы существуют, но их аналитическое выражение неизвестно.

Доказательство теорем

Прямая теорема

Любое стационарное решение бесстолкновительного уравнения Больцмана зависит от фазовых переменных только через интегралы движения. Действительно, если решение стационарно, то ФР сама является интегралом движения. Т.е либо она сама есть сохранающаяся функция фазовых координат, либо она зависит от их сохраняющихся комбинаций – интегралов движения.

Обратная теорема

Любая функция интегралов движения является решением бесстолкновительного уравнения Больцмана

\frac{d}{d t} f [I_{1} (x (t), v (t)), . . ., I_{n} (x (t), v (t))] = \sum_{m = 1}^{n} \frac{\partial f}{\partial I_{m}} \frac{d I_{m}}{d t} = 0 .

(1.51)

Изолирующие и неизолирующие интегралы

В сферически симметричном потенциале

Φ (r) = - G M (\frac{1}{r} + \frac{a}{r^{2}}),

(1.52)

сохраняются энергия и вектор углового момента. Плоскость движения частицы можно задать единичным вектором, совпадающим по направлению с вектором углового момента $n = L ∕ L$ . Движение в плоскости описывается 4-мя координатами, причем скорости выражаются через $r$ и $ψ$ . Интегрируя уравнения движения, получим:

\begin{align} \frac{1}{r} = C cos (\frac{ψ - ψ_{0}}{K}) + \frac{G M K^{2}}{L^{2}}, & (1.53) \\ K \equiv {(1 - \frac{2 G M a}{L^{2}})}^{- 1 ∕ 2}, & (1.54) \\ E = \frac{1}{2} \frac{C^{2} L^{2}}{K^{2}} - \frac{1}{2} {(\frac{G M K}{L})}^{2} . & (1.55) \\ (1.56) \end{align}

Очевидно, пятым интегралом является $ψ_{0}$ :

ψ_{0} = ψ - K A r c c o s [\frac{1}{C} (\frac{1}{r} - \frac{G M K^{2}}{L^{2}})] .

(1.57)

Теперь вопрос: можно ли, имея интегралы движения $E$ , $L$ , $ψ_{0}$ и координату $r$ , определить азимут $ψ$ ?

ψ = ψ_{0} \pm K a r c c o s [\frac{1}{C} (\frac{1}{r} - \frac{G M K^{2}}{L^{2}})] + 2 n K π .

(1.58)

Если $K = 1$ , то $ψ$ с точностью до $2 π$ определяется однозначно, и поэтому $ψ_{0}$ – изолирующий интеграл движения.

Если $K$ – иррациональное, любое наперед заданное $ψ$ может быть приближено (1.58), и поэтому $ψ_{0}$ – неизолирующий интеграл.

Неклассические интегралы

Лишь немногие галактики являются сферически симметричными. Однако многие галактики можно приближенно считать аксиально симметричными. Распределение вещества в них представляет собой фигуру вращения. Компонента вектора углового момента вдоль оси вращения сохраняется, поэтому трехмерное движение распадается на движение в меридиональной плоскости ( $R, z$ ), не зависящее от азимута, и движение по азимуту. Запишем гамильтониан

H = \frac{1}{2} (p_{R}^{2} + \frac{p_{ϕ}^{2}}{R^{2}} + p_{z}^{2}) + Φ (R, z)

(1.59)

и уравнения движения

\ddot{R} = - \frac{\partial Φ_{eﬀ}}{\partial R}, \ddot{z} = - \frac{\partial Φ_{eﬀ}}{\partial z}; Φ_{eﬀ} \equiv Φ (R, z) + \frac{L_{z}^{2}}{2 R^{2}} .

(1.60)

Примем потенциал в виде:

Φ (R, z) = \frac{1}{2} v_{0}^{2} ln (R^{2} + \frac{z^{2}}{q^{2}}),

(1.61)

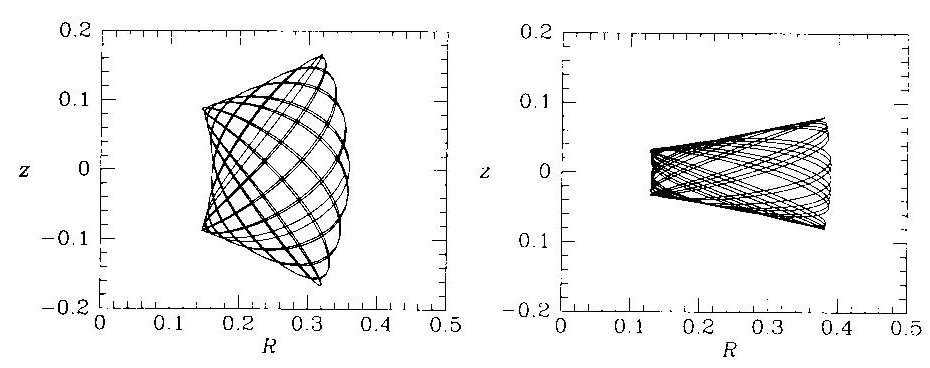
Его эквипотенциальные поверхности представляют собой сплюснутую сферу, или сфероид, при $q < 1$ . Траектории при заданных интегралах движения $E$ и $L_{z}$ могут быть различны и занимать разные области пространства, в чем легко убедиться численным интегрированием. На Рис. 1 показаны две различные траектории, полученные при одних и тех же ‘классических’ интегралах движения, но разных начальных условиях.

Рис. 1: Две траектори движения частицы, отвечающих

E = - 0.8

L_{z} = 0.2

. Параметры модели

q = 0.9

v_{0} = 1

[1].

Естественное объяснение различия траекторий состоит в том, что имеется дополнительный третий интеграл движения

I_{3} = I_{3} (R, z, p_{R}, p_{z}),

(1.62)

который принимает разные значения для начальных условий двух траекторий, показанных на Рис. 1. Уббедиться в наличии третьего интеграла можно с помощью построения поверхности сечения (сечения Пуанкаре).

Сечение Пуанкаре

Используя сохранение энергии

H_{eﬀ} (R, z, p_{R}, p_{z}) = E

(1.63)

можно выразить $p_{z}$ через остальные три координаты, т.е. имеются три независимые координаты $R, z, p_{R}$ . Но рисовать орбиты в 3-х мерном пространстве неудобно. Для наглядного представления траектории фиксируют одну из переменных, например, полагая $z = 0$ , и на плоскости $R, p_{R}$ отмечают точки, где орбита пересекает плоскость $z = 0$ . При этом, чтобы избежать неопределенности отмечают только те точки, когда пересекающая плоскость частица движется в каком-то одном направлении, например внизу вверх (т.е. $p_{z} > 0$ ). Ключевым моментом в построении поверхности сечения является то обстоятельство, что никакие две орбиты не могут проходить через одну точку. Пример такого сечения показан на Рис. 2.

Рис. 2: Сечение Пуанкаре для орбиты, показанной на Рис. 1 слева.

Сплошная линия на Рис. 2 – поверхность нулевой скорости $H_{eﬀ} = p_{R}^{2} ∕ 2 + Φ_{eﬀ}$ или $p_{z} = 0$ . Она ограничивает область возможного расположения точек пересечения. Крест отмечает положение предельной орбиты, являющейся аналогом круговой орбиты в сферически симметричном потенциале. Эта орбита предствавляет собой двумерную оболочку. Точки показывают пересечение орбиты с экваториальной плоскостью. Пунктирная линия соответствует геометрическому месту точек пересечения при сохранении модуля вектора углового момента $L$ .

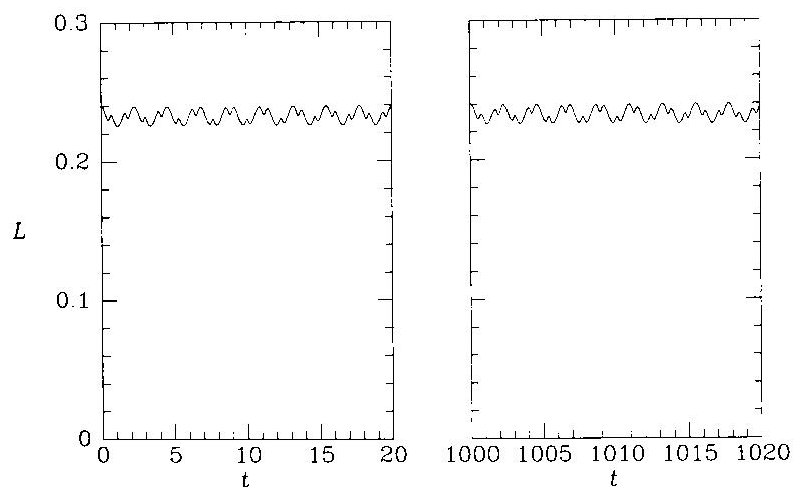
На Рис. 3 видно, что $L$ испытывает быстрые осцилляции около какого-то положения, причем это положение сохраняется на протяжении многих периодов, т.е. $L$ – приближенный интеграл движения, который имеется даже для довольно сильно уплощенных потенциалов. Орбиты звезд можно представлять себе лежащими в одной плоскости, с более-менее одинаковыми перицентрами и апоцентрами. Эти орбитальные плоскости имеют фиксированный наклон к оси $z$ , но прецессируют вокруг этой оси. Скорость прецессии уменьшается по мере того, как потенциал становится более и более сферически симметричным.

Рис. 3: Интегрирование на протяжении длительного времени показывает, что модуль углового момента совершает периодические колебания около некоторого постоянного значения.

Проблема третьего интеграла в Галактике

Если считать, что потенциал Галактики приблизительно аксиально симметричен и ФР зависит лишь от двух интегралов движения

f = f (E, L_{z}) = f (v_{r}^{2} + v_{𝜃}^{2} + v_{z}^{2} - 2 Φ, r v_{𝜃}),

(1.64)

то дисперсии скоростей по $R$ и $z$ должны быть равны

σ_{R} = σ_{z} .

(1.65)

Средние значения скоростей по $R$ и $z$ должны быть равны нулю

{\bar{v}}_{R} = {\bar{v}}_{z} = 0 .

(1.66)

Также должны быть равны нулю внедиагональные элементы:

σ_{R 𝜃} = 0 .

(1.67)

Наблюдения звезд различных возрастов показывает, что дисперсии скоростей соотносятся как $σ_{R} : σ_{𝜃} : σ_{z} \approx 1 : 0.7 : 0.5$ . С точки зрения моделей это может означать, что необходимо использовать ФР, зависящие от трех интегралов движения, либо то, что локальное распределение массы не соответствует условию аксиальной симметрии.

[next] [prev] [prev-tail] [front] [up]