Основные уравнения

1.2 Основные уравнения

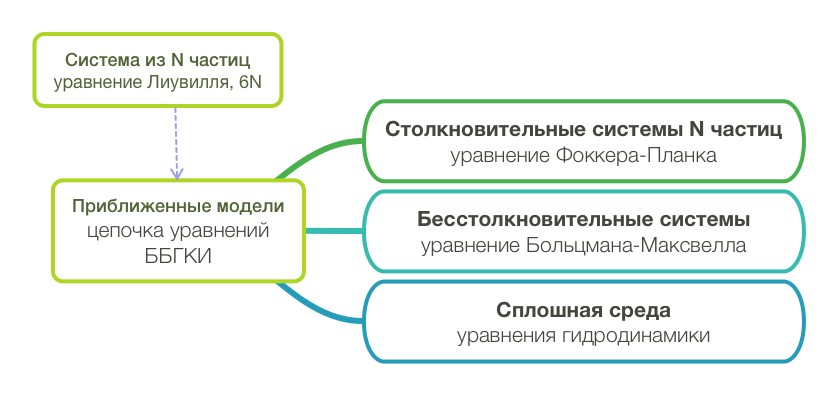
Наиболее общее описание системы $N$ взаимодействующих частиц дает уравнение Лиувилля [1, 3, 4]. Это описание точное, но на практике обычно используют приближенные модели. Цепочка Боголюбова (или Боголюбова-Борна-Грина-Кирквуда-Ивона - ББГКИ) – это бесконечная цепочка уравнений, включающих в себя одночастичную ФР $f^{(1)} (x, v, t)$ , двухчастичную ФР $f^{(2)} (x_{1}, v_{1}, x_{2}, v_{2}, t)$ и т.д., которые зацепляются между собой. Бесконечная цепочка эквивалентна описанию системы с помощью функции Лиувилля. В простейшем случае, когда корреляций между положением частиц в фазовом пространстве нет, многочастичные (т.е. 2, 3, 4, ...) ФР выражаются через $f^{(1)} (x, v, t)$ . Это позволяет обойтись лишь первым из уравнений цепочки и получить бесстолкновительное уравнение Больцмана. При учете парных корреляций получается уравнение Фоккера-Планка.

Для описания астрофизических объектов, таких как звезды, аккреционные диски, рассеянные и шаровые скопления, галактики и т.д., в основном используют два типа моделей – сплошная сжимаемая среда (газ) и система частиц, взаимодействующих по закону Ньютона (звезды). Из уравнения Больцмана (как со столкновительным интегралом, так и без) можно вывести систему гидродинамических уравнений [4C]. Эти взаимосвязи проиллюстрированы на схеме.

Газ

Газовая среда рассматривается как правило в приближении идеального газа без вязкости, который описывается плотностью $ρ (x, t)$ , давлением $p (x, t)$ и скоростью $v (x, t)$ . Последние подчиняются уравнениям гидродинамики:

уравнение непрерывности:

\frac{\partial ρ (x, t)}{\partial t} + \nabla \cdot (ρ v) = 0;

(1.19)

уравнение Эйлера:

\frac{\partial v}{\partial t} + (v \cdot \nabla) v = - \frac{1}{ρ} \nabla p - \nabla Φ;

(1.20)

уравнение состояния:

p = p (ρ) .

(1.21)

Уравнение состояния в таком виде называется баротропным. В общем случае оно представляет собой зависимость одной из термодинамических переменных от двух других (например, давление есть функция плотности и температуры). Тогда к приведенным выше уравнениям нужно добавить уравнение для локальной температуры. В этом курсе мы ограничимся лишь баротропным уравнением состояния. Политропное уравнение состояния является частным случаем баротропного, когда давление есть степенная функция плотности.

Потенциал $Φ$ в уравнении Эйлера может создаваться как внешними источниками, так и самой исследуемой системой. В последнем случае говорят о самогравитации. Если внешних сил нет, то потенциал получается путем решения уравение Пуассона

\nabla^{2} Φ = 4 π G ρ .

(1.22)

Звезды

Звездная среда будет рассматриваться нами лишь в бесстолкновительном приближении. Функция распределения (одночастичная) $f$ удовлетворяет бесстолкновительному кинетическому уравнению

\frac{d f}{d t} = \frac{\partial f}{\partial t} + v \frac{\partial f}{\partial x} - \frac{\partial Φ (x, t)}{\partial x} \frac{\partial f}{\partial v} = C (f)

(1.23)

в котором интеграл столкновений $C (f)$ положен равным нулю. Физический смысл $f$ – плотность вероятности найти частицу в точке $(x, v)$ , т.е.

f (x, v, t) d x d v

(1.24)

есть вероятность найти частицу в фазовом объеме $d x d v$ около точки $(x, v)$ . Необходимо помнить, что даже если $f$ записывается в виде $f = f (E)$ или, например, $f = f (E, L)$ , обычно имеется ввиду что это функция координат и скоростей, выраженная через интегралы движения. Иными словами, вероятность будет даваться все тем же выражением (1.24), а не $f (E) d E$ .

Если в системе имеются частицы разных масс, то ФР должна зависеть и от массы частиц. Ограничимся лишь частицами одной массы. В этом случае обычно интегралы движения (энергию, угловой момент и т.д.) записывают в виде, деленном на массу частицы:

E = \frac{v^{2}}{2} + Φ (x), L = r \times v .

(1.25)

Распределение вероятности найти частицу в объеме $d x$ около точки $x$ получается интегрированием ФР по скоростям

ν (x, t) = \int f (x, v, t) d^{3} v .

(1.26)

По смыслу плотности вероятности $f$ в этом случае нормирована на единицу, т.е.

\int f (x, v, t) d^{3} x d^{3} v = 1 .

(1.27)

Однако часто нормировку удобно изменить так, чтобы ФР была нормирована на количество частиц, полную массу или светимость системы. Например, если $N$ – полное число частиц, $M$ – полная масса, то

ν (x, t) \to n (x, t), \int n (x, t) d^{3} x = N; ν (x, t) \to ρ (x, t), \int ρ (x, t) d^{3} x = M .

(1.28)

Системой уравнений Власова называется пара уравнений (1.22) и (1.23) с $C = 0$ .

Для нахождения равновесных газовых систем используют стационарные уравнения гидродинамики (1.19–1.21) и уравнение Пуассона (1.22); при исследовании на устойчивость – линеаризованные нестационарные уравнения. В случае бесстолкновительных звездных систем используют систему уравнений Власова.

Отсутствие столкновений означает, что каждая частица взаимодейсивует с гладким коллективным гравитационным полем. Поскольку ФР определяет потенциал, который также входит в уравнение Больцмана, даже в бесстолкновительном случае задача нахождения равновесной конфигурации оказывается, вообще говоря, нелинейной.

Из-за того, что потенциал не совсем гладкий (он складывается из множества потенциалов отдельных частиц), частицы отклоняются от тех траекторий, которые они имели бы в гладком потенциале. В реальности действующую на каждую частицу силу можно представить в виде суммы плавно меняющейся силы от гладкого потенциала и небольшой случайной силы, обязанной наличию дискретности распределения (конечности $N$ ). Характерная шкала времени на которой наличие флуктуаций существенно меняет траекторию, определяется временем релаксации $t_{rel}$

t_{rel} \sim 0.1 \frac{N}{log N} t_{dyn},

(1.29)

где $t_{dyn}$ – динамическое время, для трехмерных систем типа сфер [1]. Отклонение траектории пробной частицы от ее траектории в гладком потенциале происходит в основном за счет слабых взаимодействий c дальними частицами, а не более сильных взаимодействий с соседними. Именно поэтому в знаменателе появляется Кулоновский логарифм $log N$ .

В плоских системах ситуация значительно отличается от трехмерной [White R., ApJ 330, 26, 1988]. Так, если сила взаимодействия точно $\propto 1 ∕ r^{2}$ , то время релаксации

t_{rel,0} \sim κ^{- 1} \sim t_{dyn},

(1.30)

где $κ$ – частота радиальных колебаний (эпициклическая частота). При наличии смягчения, т.е. когда сила взаимодействия $\propto r ∕ {(r^{2} + h^{2})}^{3 ∕ 2}$ ,

t_{rel} \approx N \frac{h}{R_{d}} \frac{σ^{2} R_{d}}{G M_{d}} t_{rel,0},

(1.31)

где $h$ – характерная длина смягчения гравитации, $M_{d}$ и $R_{d}$ – масса и радиальная шкала диска, $σ$ - радиальная дисперсия скоростей. Отношение $h ∕ R_{d}$ мало, как и отношение $σ^{2} R_{d} ∕ G M_{d}$ , имеющее в диске порядок отношения квадрата радиальной дисперсии к квадрату круговой скорости. Несмотря на это, при большом $N$ время релаксации $t_{rel}$ можно сделать много большим характерного времени радиальных колебаний ( $\sim t_{dyn}$ ) .

[next] [prev] [prev-tail] [front] [up]