Равновесные распределения

3.1 Равновесные распределения

3.1.1 Однородный слой

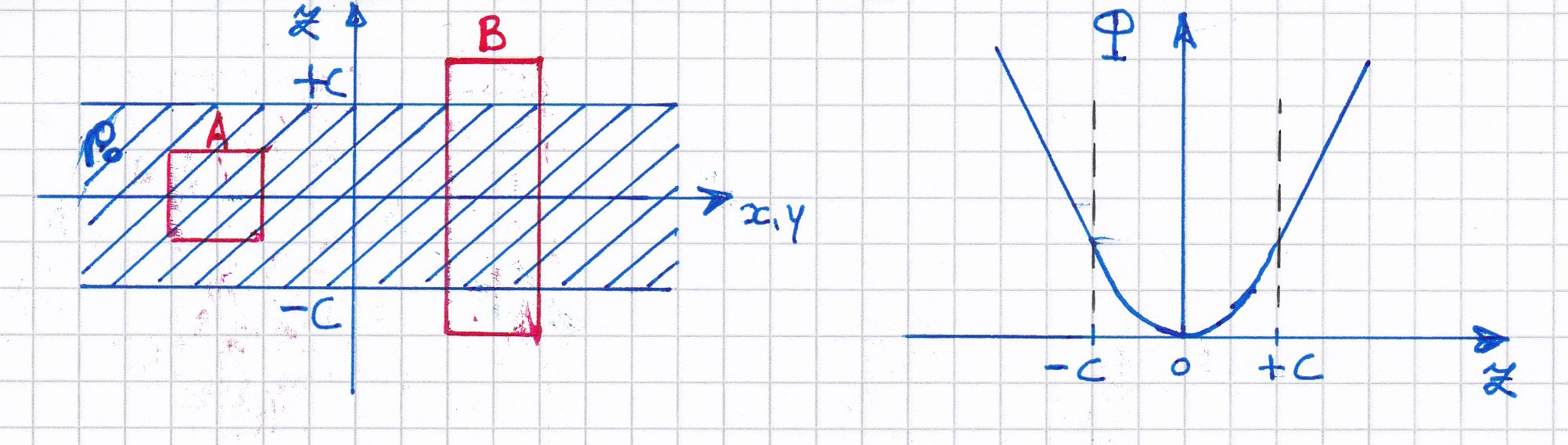
Рассмотрим однородный слой с объемной плотностью $ρ_{0}$ , занимающий область пространства $| z | \leq c$ (см. Рис. 6.) Поверхностная плотность

Σ_{0} = \int_{- \infty}^{\infty} d z ρ (z) = 2 ρ_{0} c .

(3.1)

Найдем потенциал с помощью уравнения Пуассона

Δ Φ = 4 π G ρ_{0} 𝜃_{H} (c^{2} - z^{2}) .

(3.2)

По теореме Остроградского-Гауссса:

\int d i v \nabla Φ d v = \oint \nabla Φ \cdot d s = 4 π G r_{0} \int 𝜃_{H} (c^{2} - z^{2}) d^{3} v .

(3.3)

В силу симметрии очевидно, что силовое поле направлено к слою и его линии идут перпендикулярно плоскости $z = 0$ . Поэтому потенциал зависит только от переменной $z$ , а лапласиан

Δ = \nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}

(3.4)

заменяется просто на $d^{2} ∕ d z^{2}$ . Выбирая объем интегрирования внутри слоя в виде цилиндра A (Рис. 6), расположенного симметрично относительно начала оси $z$ , с площадью основания $S$ и образующей $2 z$ , имеем

2 S {(\nabla Φ)}_{z} = 4 π G ρ_{0} S \cdot (2 z),

(3.5)

или

(\nabla Φ_{z}) = 4 π G ρ_{0} z,

(3.6)

откуда, полагая $Φ (0) = 0$ , получим.

Φ_{z} = 2 π G ρ_{0} z^{2} .

(3.7)

Рис. 6: Слева: однородный слой с плотностью

ρ_{0}

и полутолщиной

c

: A – цилиндр внутри слоя, B – цилиндр, выходящий за пределы слоя. Справа – зависимость потенциала слоя от

z

(внутри слоя – квадратичная, вне слоя – линейная).

Потенциал вне слоя найдем аналогично. Образующая цилиндра B теперь $2 z > 2 c$ :

2 S {(\nabla Φ)}_{z} = 4 π G ρ_{0} S \cdot (2),

(3.8)

откуда имеем

(\nabla Φ_{z}) = 4 π G ρ_{0} c .

(3.9)

Сшивая решение для потенциала вне слоя с решением внутри слоя, получим

Φ_{z} = \{\begin{matrix} 2 π G ρ_{0} z^{2}, & | z | < c \\ 2 π G ρ_{0} c (2 | z | - c), & | z | \geq c \end{matrix} .

(3.10)

Пусть $Ω_{0}$ – частота вертикальных колебаний частицы внутри слоя. Тогда

Φ = \frac{Ω_{0}^{2} z^{2}}{2} = 2 π G ρ_{0} z^{2}, Ω_{0}^{2} = 4 π G ρ_{0}

(3.11)

Функция распределения

f = f (E_{z}), E_{z} = \frac{v^{2}}{2} + \frac{Ω_{0}^{2} z^{2}}{2}

(3.12)

должна обращаться в нуль на краю слоя, т.е. при $E_{z} \geq Ω_{0}^{2} c^{2} ∕ 2$ и удовлетворять одномерному бесстолкновительному кинетическому уравнению вдоль оси $z$ :

v_{z} \frac{\partial f_{0}}{\partial z} - Ω_{0}^{2} z \frac{\partial f_{0}}{\partial v_{z}} = 0 .

(3.13)

Для того, чтобы найти функцию распределения, запишем условие самосогласования:

ρ = \int f_{0} d v_{z} = ρ_{0} 𝜃_{H} (c^{2} - z^{2})

(3.14)

где $h$ – функция Хевисайда, а интегрирование по $v_{z}$ сводится к интервалу, на котором $E_{z} < Ω_{0}^{2} c^{2} ∕ 2$ . Введем новые переменные $J$ и $x$ :

J = Ω_{0}^{2} c^{2} - 2 E_{z}, x = Ω_{0}^{2} (c^{2} - z^{2}),

(3.15)

тогда

v_{z} = {(2 E_{z} - Ω_{0}^{2} z^{2})}^{1 ∕ 2} = {(Ω_{0}^{2} (c^{2} - z^{2}) - J)}^{1 ∕ 2} = {(x - J)}^{1 ∕ 2}

(3.16)

ρ (x) = ρ_{0} 𝜃_{H} (c^{2} - z^{2}) = \int_{- x^{1 ∕ 2}}^{x^{1 ∕ 2}} f (E_{z}) d v_{z} = 2 \int_{0}^{x^{1 ∕ 2}} f (E_{z}) d v_{z} = \int_{0}^{x} f_{0} (J) \frac{d J}{{(x - J)}^{1 ∕ 2}} .

(3.17)

Полученное уравнение на $f_{0}$ есть уравнение Абеля, которое имеет решение в общем виде:

f_{0} (J) = \frac{1}{π} \frac{d}{d J} \int_{0}^{J} \frac{ρ (x) d x}{\sqrt{J - x}}

(3.18)

Вычисляя интеграл, получим

f_{0} (J) = \{\begin{matrix} \frac{ρ_{0}}{π} \frac{d}{d J} (2 \sqrt{J}) = \frac{1}{π \sqrt{J}}, & J > 0, \\ \frac{ρ_{0}}{π} \frac{d}{d J} 0 = 0, & J < 0, \end{matrix}

(3.19)

или

f_{0} (J) = \frac{ρ_{0}}{π} \frac{𝜃_{H} (J)}{J^{1 ∕ 2}}, J \equiv Ω_{0}^{2} (c^{2} - z^{2}) - v_{z}^{2} .

(3.20)

Можно считать, что $f_{0}$ зависит также от $v_{x}$ и $v_{y}$ , т.е. $f_{0} = f_{0} (J, v_{x}, v_{y})$ , поскольку эти компоненты скорости сами являются в данном случае интегралами движения. Особенность ФР $\propto J^{- 1 ∕ 2}$ происходит из необходимости обеспечить резкую границу распределения плотности при $| z | = c$ .

3.1.2 Изотермический слой

Рассмотрим пример распределения материи в виде плоского слоя, но с плавным распределением плотности. ФР выберем в виде

f = \frac{ρ_{0}}{{(2 π σ_{z}^{2})}^{1 ∕ 2}} exp (- \frac{E_{z}}{σ_{z}^{2}}), E_{z} = \frac{v_{z}^{2}}{2} + Φ (z)

(3.21)

что приводит к распределению плотности

ρ = ρ_{0} e^{- Φ ∕ σ_{z}^{2}} .

(3.22)

Введем новые безразмерные переменные

ϕ = \frac{Φ}{σ_{z}^{2}}, ζ = \frac{z}{z_{0}}, z_{0}^{- 1} = \frac{{(8 π G ρ_{0})}^{1 ∕ 2}}{σ_{z}}

(3.23)

и перепишем уравнение Пуассона:

2 \frac{d^{2} ϕ}{d ζ^{2}} = e^{- ϕ}

(3.24)

которое необходимо решить при начальных условиях

ϕ = 0, ϕ^{'} = 0 .

(3.25)

Домножая на $ϕ^{'}$ и интегрируя, получим последовательно

2 ϕ^{″} ϕ^{'} - ϕ^{'} e^{- ϕ} = 0, \frac{d {ϕ^{'}}^{2}}{d ζ} + \frac{d e^{- ϕ}}{d ζ} = 0, {(ϕ^{'})}^{2} + e^{- ϕ} = C .

(3.26)

Константу интегрирования можно найти с помощью начальных условий ( $C = 1$ ), откуда

ϕ^{'} = \sqrt{1 - e^{- ϕ}}, d ζ = \frac{d ϕ}{\sqrt{1 - e^{- ϕ}}} .

(3.27)

Далее последовательно умножая на $e^{ϕ ∕ 2}$ и делая замены переменных $e^{ϕ ∕ 2} \to τ$ , $τ \to c h t$ , получаем

d ζ = \frac{e^{ϕ ∕ 2} d ϕ}{\sqrt{e^{ϕ} - 1}} = \frac{2 d τ}{\sqrt{τ^{2} - 1}} = \frac{2 s h (t) d t}{\sqrt{c h^{2} (t) - 1}} = 2 d t,

(3.28)

или $ζ = 2 t + C_{1}$ . Константа интегрирования $C_{1} = 0$ , т.к. при $z = 0$ безразмерный потенциал $ϕ = 0$ , а следовательно $t = 0$ . Итак, мы получили

τ = c h t = c h ζ ∕ 2,

(3.29)

Φ = 2 σ_{z}^{2} ln c h (ζ ∕ 2), ρ = ρ_{0} e^{- ϕ} = \frac{ρ_{0}}{c h^{2} (ζ ∕ 2)}, ζ = \frac{z}{σ_{z}} {(8 π G ρ_{0})}^{1 ∕ 2}

(3.30)

Поверхностная плотность получается интегрированием по $z$ :

Σ_{0} = \int_{- \infty}^{\infty} d z ρ (z) = 4 ρ_{0} z_{0} .

(3.31)

При $| ζ | ≫ 1$ имеем $ln c h (ζ ∕ 2) \approx | ζ | ∕ 2$ , откуда $Φ \approx 8 π G ρ_{0} z_{0} | z |$ . Сравнение с (3.10) показывает, что $2 z_{0}$ соответствует $c$ из предыдущего раздела. Это согласуется с формулами (3.1) и (3.31).

[next] [prev] [prev-tail] [front] [up]