Path
alex >>> /Users/epolyach/Dropbox/Urtica/Gas_FEM; /Users/epolyach/Dropbox/WORK/Gaseous_modes perseus >>> /home/Tux/epolyach/GAS_FEM/CED0
FEM for gaseous discs
Here I show some issues I bumped while calculating modes in the gaseous disc with pressure and zero softened gravity, \(Q=1\).
FEM provides “major” and “minor” modes. The major modes are labelled by letters: R, A, B, C, D, E, F, G corresponding to the decrease of the pattern speed:
| mode | \(R_\textrm{max}=16\) | \(R_\textrm{max}=32\) | \(R_\textrm{max}=16\) | \(R_\textrm{max}=32\) |
| R | 0.968987 | 0.968987 | 0.088579 | 0.088578 |
| A | 0.426048 | 0.426013 | 0.044900 | 0.044493 |
| B | 0.415210 | 0.415215 | 0.068317 | 0.068300 |
| C | 0.326370 | 0.326541 | 0.012101 | 0.012687 |
| D | 0.317860 | 0.317860 | 0.088313 | 0.088313 |
| E | 0.255012 | 0.255011 | 0.067981 | 0.067981 |
| F | 0.192069 | 0.192096 | 0.034633 | 0.034619 |
| G | 0.127193 | 0.127313 | 0.002217 | 0.002057 |
I use three codes, S6, PG, and MN that differ in the weight functions \(\mu, \nu\) (see also subsection 'Codes’). For PG I use \(\mu=\nu=\Sigma_0(R)\), while S6 code has simply \(\mu=\nu=1\).
Minor modes issue – N_d dependence
For N_d=4, minor modes attain growth rate 0.0225 (number of modes is N_m=25) for \(R_\textrm{max}=16\), and 0.009 (N_m=61) for \(R_\textrm{max}=32\). This is different from what I have in the version I of the paper [0.0176 (76) and 0.076 (33)].
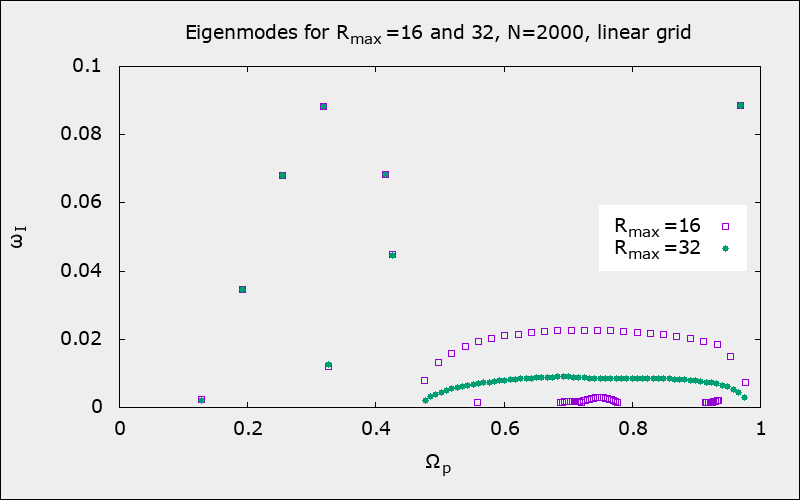 |
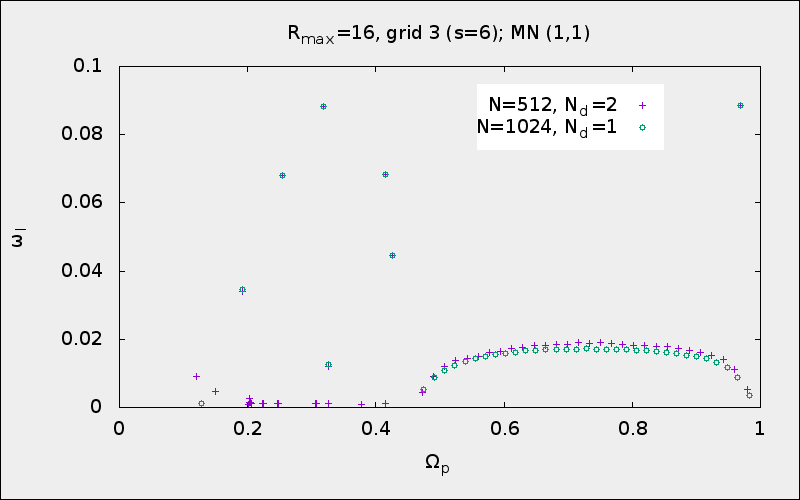
My experiments show that the maximum growth rate increases and their number decreses when one switches from N_d=1 to N_d=4. In particular, for N_d=2, max growth rate is 0.0085, the number of modes is 67 (although, there are garbage modes with relatively high growth rates, so I might miss one or two minor modes).
 |
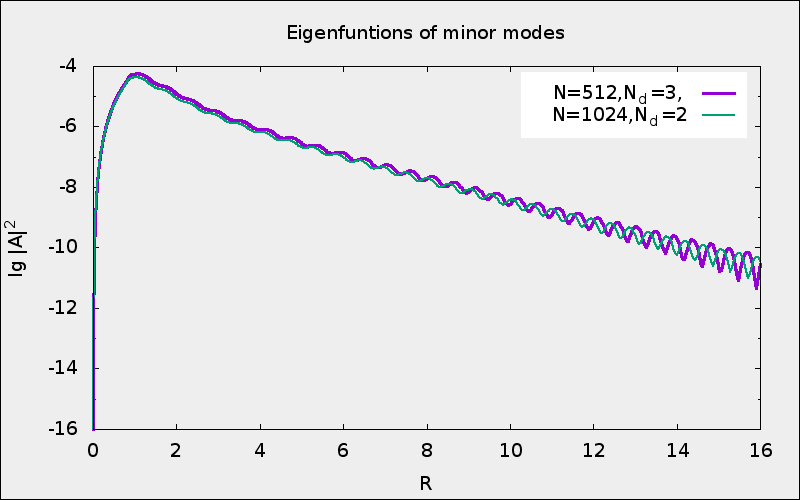
Eigenfunctions are different:
 |
Numerical instability
Green points of minor modes are localized both to the left and to the right from the boundary \(\Omega_\textrm{p}=0.462\) separating emitters from absorbers:
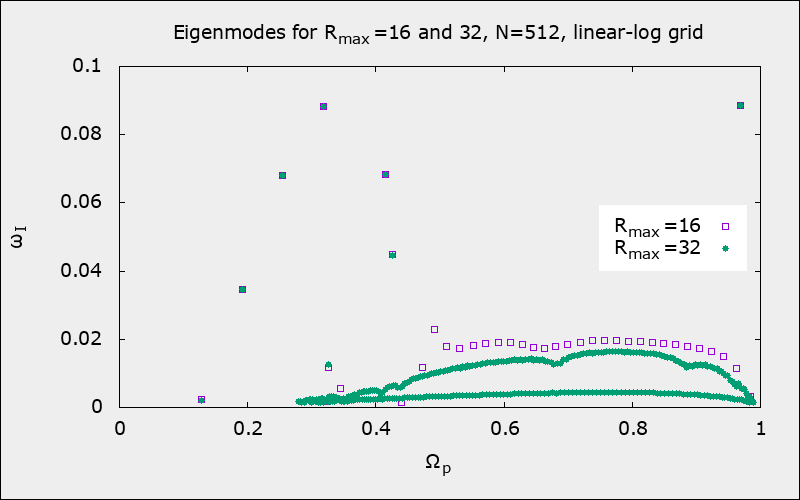 |
Examination of the eigenfunctions shows that this is a result of numerical instability due to insufficient number of nodes.
Here is a typical regular eigenfunction \((\Omega_\textrm{p}, \omega_\textrm{I})=(0.738, 0.020)\):
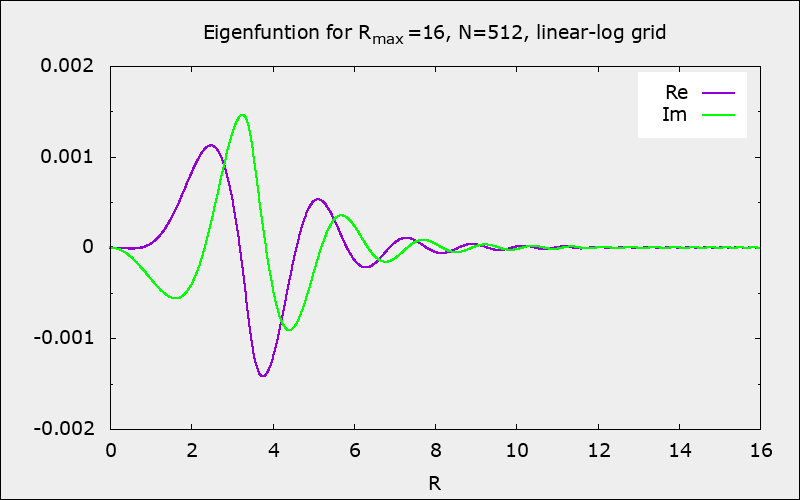 |
Here is an effect of numerical instability \((\Omega_\textrm{p}, \omega_\textrm{I})=(0.738, 0.016)\) – filled areas are oscillations of the functions:
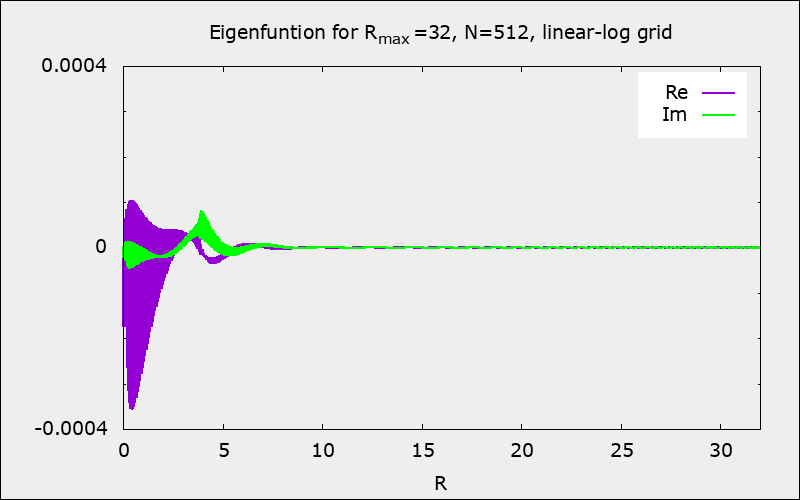 |
Grid
Comparison of lin-log grid and linear grid; S6 code
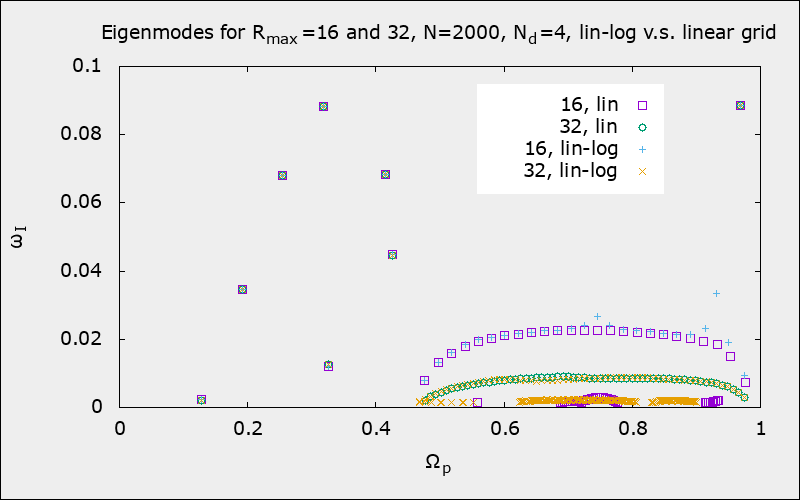 |
Codes
@ ~/Dropbox/Urtica/Gas_FEM:
- gas_FEM_PG_Rmax_perseus.m
solves matrix equation for \(u\), \(v\), \(\eta\); weights \(\mu=\nu=(1+\tau\Sigma_0(R))\), \(\tau\) is usually taken \(10^8\).
@ perseus : /home/Tux/epolyach/GAS_FEM/CED0
- gas_FEM_S6_Rmax_perseus.m
solves matrix equation for \(u\), \(v\), \(\eta\); weights \(\mu=\nu=1\).
@ ~/Dropbox/Urtica/Gas_FEM:
- gas_FEM_MuNu_Rmax.m
solves matrix equation for \(u\), \(v\), \(\eta\); weights \(\mu\), \(\nu\) are arbitrary analytic functions.
Grids
I use grids:
linear (\(R_\textrm{min}\), \(R_\textrm{max}\), \(N+1\))
log (\(R_\textrm{min}\), \(R_\textrm{max}\), \(N+1\))
linear–log: \(R_j = R_s (e^{q \tau_j} - 1)\).
Matlab usage
| Node | N*N_d | Memory, Gb | Time, h (matrix inv.) |
| perseus | 8000 | 66 | 25.3 (24.8) |
| edita | 4000 | 21 | 4.06 (3.96) |
| edita | 2048 | 10 | 0.96 (0.92) |
Nodes
perseus : Intel(R) Xeon(R) CPU E5-2667 v2 @ 3.30GHz 8 cores, RAM 128 Gb edita : Intel(R) Xeon(R) CPU E3-1240 v5 @ 3.50GHz 4 cores, RAM 32 Gb MBP : Intel(R) Core(TM) i7-7820HQ CPU @ 2.90GHz 4 cores, RAM 16 Gb