Code paper
This is disc-bulge-halo model build with Eugene Vasiliev's particle generator.
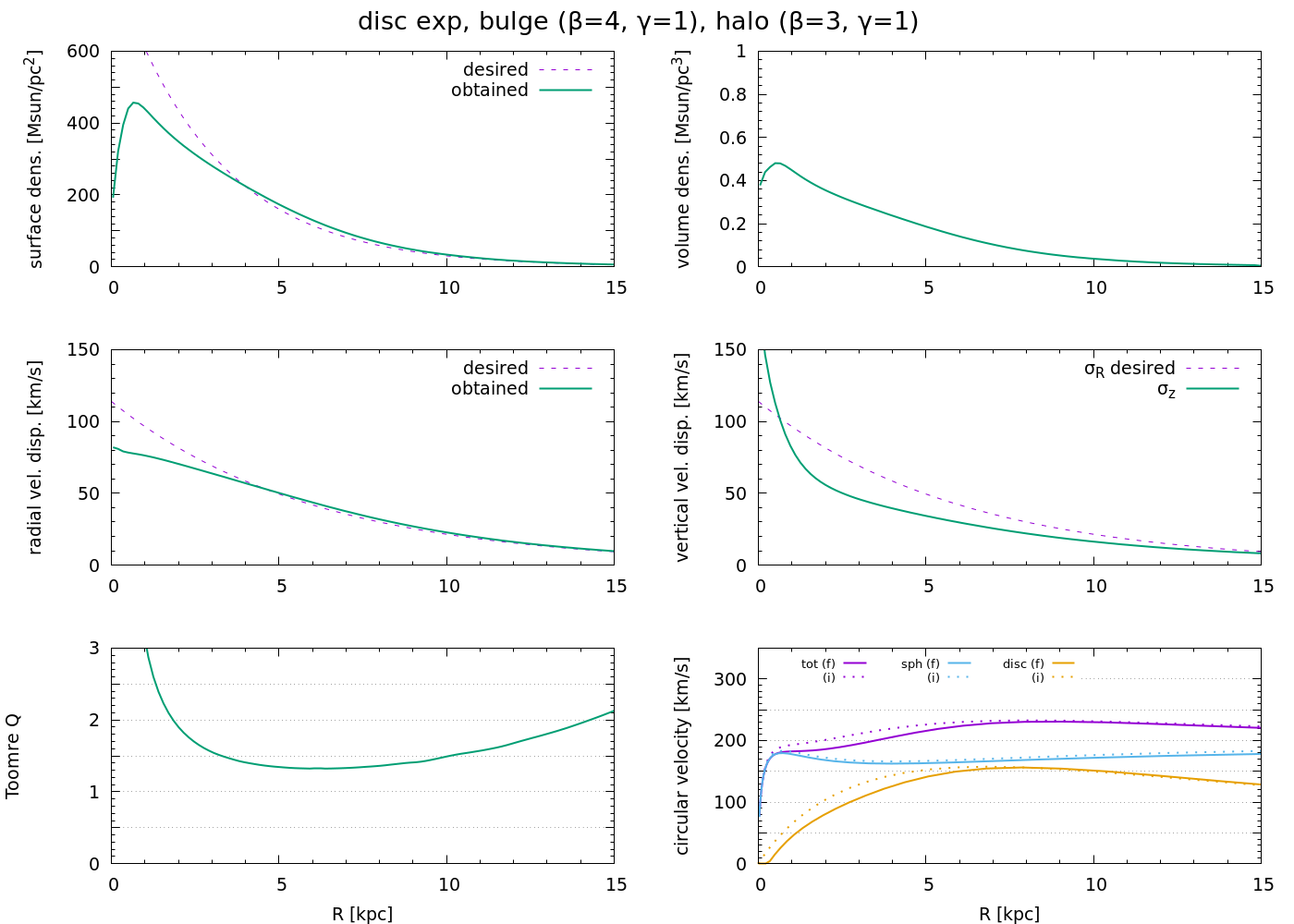
Exponential disc
\[ f(J) = \frac{1}{(2\pi)^3} f_\varphi (J_\varphi) f_R (J_r, J_\varphi) f_z (J_z, J_\varphi)\ , \]
where
\[ f_\varphi = 4 \pi M_\textrm{disc} \frac{\Omega}{\kappa^2} \exp\left( -R/R_\textrm{disc} \right)\ , \\ f_r = \frac{\sigma_r^2} \kappa \exp\left( - \kappa J_r / \sigma_r^2 \right)\ , \\ f_z = \frac{\sigma_z^2} \nu \exp\left( - \nu J_z / \sigma_z^2 \right)\ . \]
Radial velocity dispersion:
\[ \sigma_r = \sigma_{r,0} \exp\left[ -R / ( R_\sigma ) \right]\ . \]
Vertical velocity dispersion:
\[ \sigma_z = \sqrt{2} h \nu\ , \]
where \(h\) is the disc thickness.
| \(M_\textrm{disc}\), \(10^{9}\)M\(_\odot\) | 48 |
| \(\Sigma_{d,0}\), M\(_\odot\)pc\(^2\) | 0.3651 |
| \(R_\textrm{disc}\), kpc | 3.0 |
| \(R_\sigma\), kpc | 6.0 |
| \(h\), pc | 250 |
| \(\sigma_{r,0}\), kms | 114 |
| \(N_\textrm{disc}\) | 65536 |
Bulge and halo
For bulge and halo we adopt SpheroidDensity model, which is an extension of the two-power profile (BT, p.70):
\[ \rho(r) = \rho_0 \left(\frac\mu a \right)^\gamma \left( 1+ \left(\frac\mu a\right)^\alpha \right)^{\displaystyle \frac{\gamma-\beta}\alpha } \exp\left[-\left( \frac{\mu}{r_\textrm{cut}}\right)^\xi \right] \]
where
\[ \mu^2 \equiv x^2 + (y/p)^2 + (z/q)^2\ . \]
If not stated, default values apply (usually 1).
Hernquist bulge
| \(M_\textrm{bulge}\), \(10^{9}\)M\(_\odot\) | 12 |
| \(a\), kpc | 0.6 |
| \(r_\textrm{cut}\), kpc | 4.5 |
| \(\beta\) | 4 |
| \(\gamma\) | 1 |
| \(q\) | 1 |
| \(N_\textrm{bulge}\) | 16384 |
NFW halo
| \(M_\textrm{halo}\), \(10^{9}\)M\(_\odot\) | 708 |
| \(a\), kpc | 15 |
| \(r_\textrm{cut}\), kpc | 150 |
| \(\beta\) | 3 |
| \(\gamma\) | 1 |
| \(q\) | 1 |
| \(N_\textrm{halo}\) | 966656 |
| \(N_\textrm{tot}\) | 1048576 |
Potential multipole expansion
\[ \Phi(r, \theta) = \sum\limits_{l=0}^{l_\textrm{max}} \sqrt{2l+1} \Phi_{l,0} (r) P_l (\cos\theta)\ , \]
where \(\Phi_{l,0} (r)\) are tabulated in rotcurve_iter5_0, \(P_l(x)\) are Legendre polynomials:
\[ P_0(x) = 1 \ ,\\ P_1(x) = x \ ,\\ P_2(x) = (3x^2-1)/2 \ , \\ P_3(x) = (5x^2-3)x/2 \ , \\ P_4(x) = (35x^4-30x^2+3)/8 \ , \]
\(0\leq \theta \leq \pi\).
 |
Particle distribution
1:4:59