a)
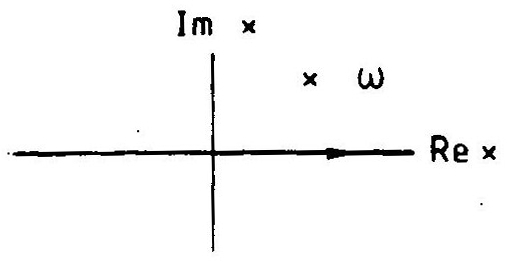 b)
b)
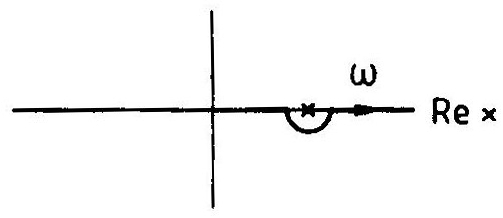 c)
c)
Рассмотрим равновесное состояние бесконечной однородной звездной среды, заданное максвелловской ФР
| (2.23) |
где , – дисперсия скоростей, одинаковая во всех направлениях. По аналогии с газовой средой определим джинсовское волновое число, заменив скорость звука на :
| (2.24) |
Пока это просто обозначение для ; его роль будет видна в дальнейшем. Запишем линеаризованное бесстолкновительное уравнение Больцмана, используя трюк Джинса ().
| (2.25) |
Умножая это уравнение на , интегрируя по пространственным координатам и используя теорему Гаусса (предполагая, что обращается в нуль на бесконечности), получим
| (2.26) |
| (2.27) |
Так как при возмущение отсутствует, интегрирование (2.26) дает:
| (2.28) |
Интегрируя последнее по пространству скоростей и заменяя на плотность (с помощью уравнения Пуассона), получим
| (2.29) |
или в виде свертки
| (2.30) |
с функцией
| (2.31) |
где – функция Хевисайда. В частности, для максвелловской ФР
| (2.32) |
Преобразование Фурье функции общего вида (2.31) дает
| (2.33) |
По теореме о свертке для (2.30) имеем
| (2.34) |
откуда получаем дисперсионное уравнение:
| (2.35) |
ДУ можно проанализировать, взяв максвелловскую ФР и выбрав удобным способом систему координат. Введем декартовы координаты так, чтобы первая ось координат была параллельна и проинтегрируем ФР по :
| (2.36) |
Тогда можно записать в виде:
| (2.37) |
Интеграл сходится, т.к. , а интегрирование ведется по действительной оси .
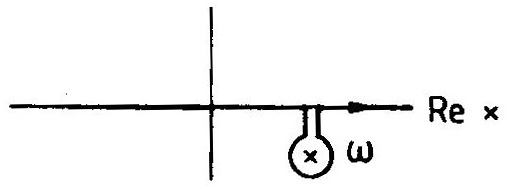
Функция может быть аналитически продолжена в область деформацией контура интегрирования, который должен проходить ниже полюса подынтегральной функции, см. Рис.4, т.е. переменная интегрирования принимает комплексные значения.
a)
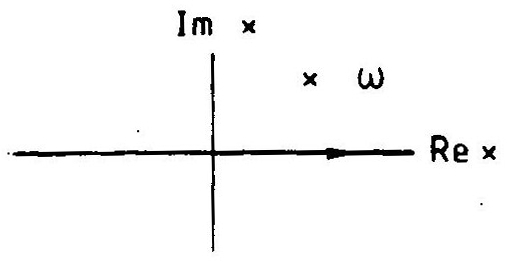 b)
b)
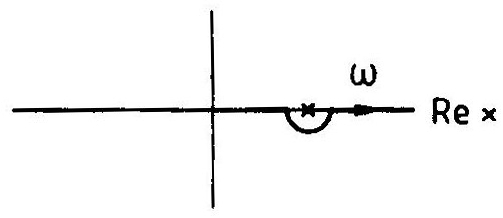 c)
c)

Для произвольных функцию можно записать в виде
| (2.38) |
где интегрирование ведется по контуру Ландау . Используя теорему о вычетах, запишем
| (2.39) |
где v.p. означает взятие интеграла в смысле главного значения.
Для максвелловской ФР
| (2.40) |
поэтому
| (2.41) |
Обозначим через дисперсионную функцию плазмы (или функцию Крампа):
| (2.42) |
Ее можно представить через функцию ошибок :
| (2.43) |
причем это представление уже имеет правильное аналитическое продолжение на всю комплексную плоскость . Тогда запишестся в виде:
| (2.44) |
откуда получаем дисперсионное уравнение:
| (2.45) |
Рассмотрим решения при различных .
Неустойчивые решения ()
Из (2.44) следует, что , т.е.
| (2.46) |
т.е. интеграл должен обращаться в нуль. Из соображений симметрии ясно, что , поэтому , и
| (2.47) |
При инкремент нарастания , что оправдывает введение джинсовского волнового числа для звездной среды согласно (2.24): разграничивает устойчивые и неустойчивые типы решений.
Нейтральные колебания (, )
Дисперсионная функция плазмы для действительных
| (2.48) |
Интеграл в смысле главного значения – действителен, а мнимая часть содержится только в добавке от полувычета. Поэтому из следует . Т.е. решений, отвечающих нейтральным колебаниям, нет.
Поскольку неустойчивые решения есть при , а нейтральных колебаний нет, то все возмущения при должны затухать. Численное расчет показывает, что таких решений бесконечно много, см. Рис. 6.