5.4 Дифференциальное вращение. Основные резонансы галактического диска

Как мы видели на примере однородной бесстолкновительной звездной среды, резонансы играют исключительную роль в свойствах среды в целом. Начиная исследование устойчивости газового и звездного дисков, необходимо определить, какие резонансы имеются в системе. Для простоты рассмотрим галактический диск как вращающуюся среду, состоящую из одной компоненты; толщину диска будем считать равной нулю и все частицы среды пусть движутся в одной плоскости. Скорость вращения частиц задается кривой вращения $v_c\left(R\right)$ или угловой скоростью $\Omega \left(R\right)=v_c\left(R\right)∕R$. Движение вещества в галактике дифференциальное, т.е. $\Omega =\Omega \left(R\right)$ зависит от радиуса $R$.

В отличие от однородной бесконечной среды, где описание возмущений удобно производить при помощи разложения по плоским волнам, во вращающихся средах используются цилиндрические координаты и разложение по азимутальному углу $\phi$.

Движение звезды в аксиально-симметричном плоском диске квазипериодическое: колебания по радиусу и по азимуту периодические, но из-за того, что отношение частот колебаний по радиусу и по азимуту не обязательно рациональное число, это движение не является периодическим. Для их описания удобно использовать переменные действие–угол:

Гамильтониан системы можно выразить через переменные действия:

Переменные действия $J_R,J_{\phi }$ задают форму орбиты. Частоты радиальных и азимутальных колебаний равны:

Условие для резонансов

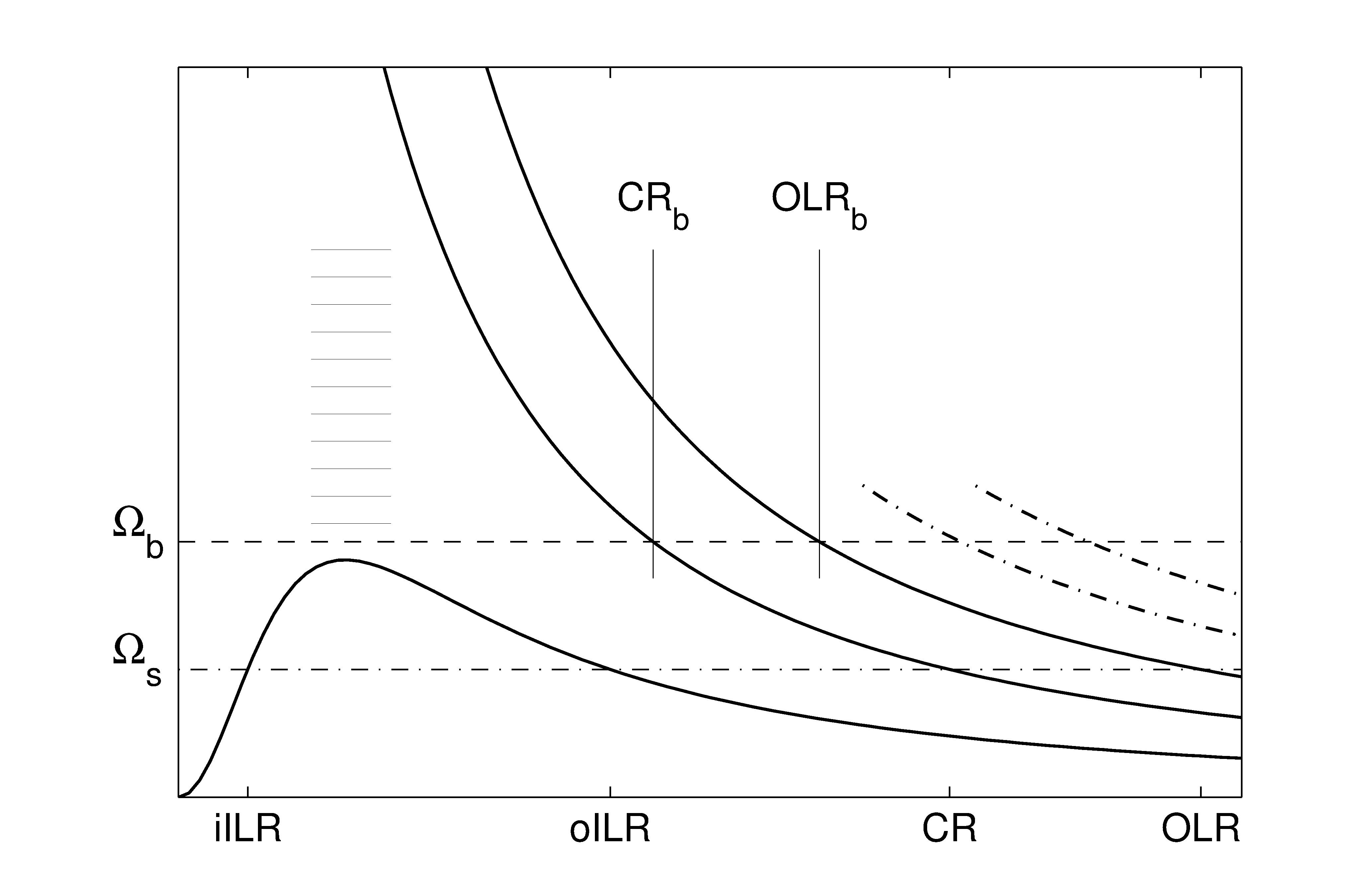
$n,m$ – произвольные целые числа. Резонансные условия определяют гиперповерхности в прострастранстве действий $J$ (линии, поверхности, ...). В частном случае, когда движения звезд происходит по почти круговым орбитам, ${\Omega }_1\left(J\right)\to \kappa \left(r\right)$, ${\Omega }_2\left(J\right)\to \Omega \left(r\right)$, а положения резонансов определяется расстоянием от центра. Резонансы играют важную роль в динамике галактик, в частности в их устойчивости. На Рис. 14 показаны основные резонансы галактического диска (коротационный и линдбладовские) для модели Пламмера.

Рис. 14: Угловая скорость вращения $\Omega \left(r\right)$, кривые $\Omega \left(r\right)\pm \frac{\kappa \left(r\right)}{2}$ в модели Пламмера. Пересечение с ${\Omega }_{\mathrm{\text{p}}}={\Omega }_{\mathrm{\text{b,s}}}$ показывает положение коротационного резонанса (CR) и линдбладовских резонансов (ILR, OLR) двухрукавной спиральной волны $m=2$.