4.6 Сравнение $N$-body моделирования с теоретическими расчетами неустойчивых мод

Неустойчивость звездных систем можно исследовать как путем моделирования задачи $N$ тел, так с помощью теоретических расчетом, используя так называемые матричные уравнения линейной теории устойчивости. Для сферических систем есть два вида последних: нелинейные [Поляченко В.Л. и Шухман И.Г. Астрон. журн. 58, 933 (1981)] и линейные [Polyachenko E.V., Polyachenko V.L., Shukhman I.G. MNRAS, 379, 573 (2007)].

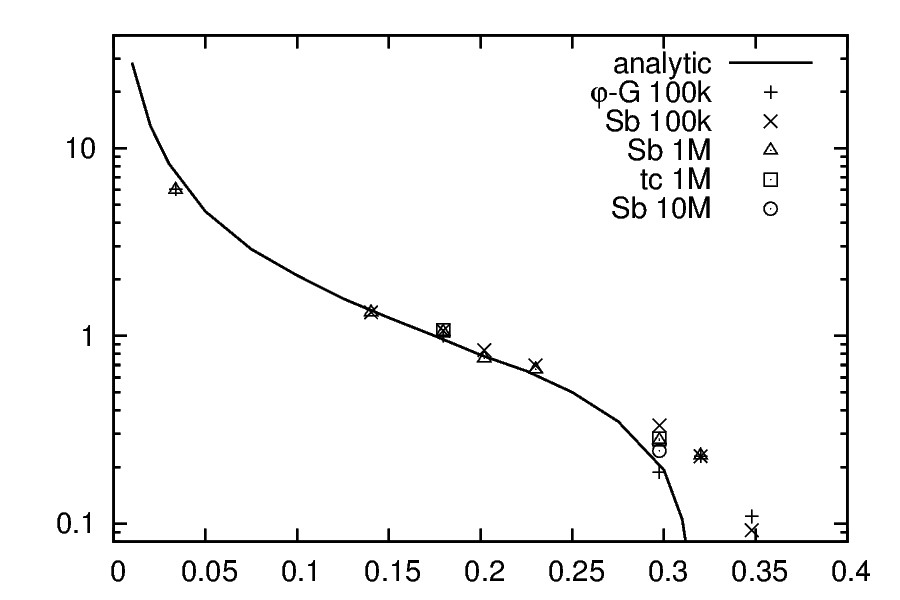
На Рис. 4.6 показаны результаты расчетов инкрементов нарастания возмущений $l=2$ в несингулярных политропных моделях при $q=0$ полученные матричным методом и с помощью моделирования задачи $N$ тел. Сравнение различных способов вычисления икрементов показывает неплохое согласие, особенно когда инкременты не очень малы. На границе устойчивости инкременты нарастания обращаются в нуль, и вблизи границы устойчивости $L_T=0.316$ необходимо использовать большее количество частиц в задаче $N$ тел.

Рис. 11: Инкременты нарастания $\gamma$ возмущений $l=2$ неустойчивости радиальных орбит в несингулярных политропных моделях при $q=0$, полученные матричным методом (сплошная линия) и с использованием различных схем численного моделирования задачи $N$ тел (Sb – SuperBox, $\phi$-G – $\phi$-GRAPE, tc – treecode; 100k - $N=10^5$ частиц, и т.д.) .

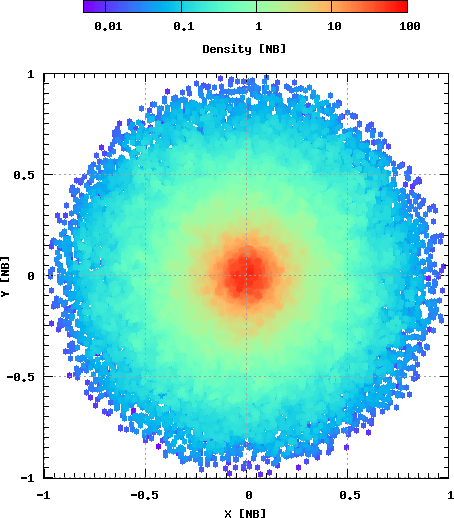
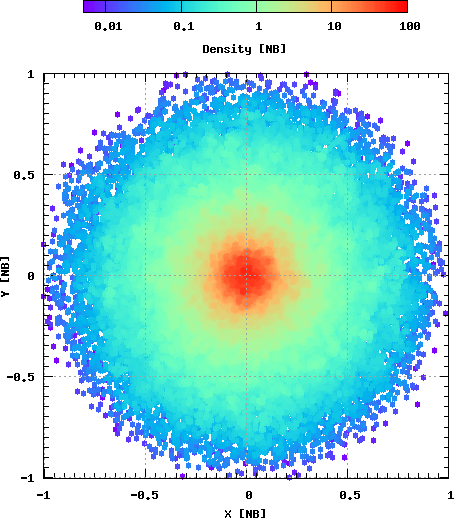
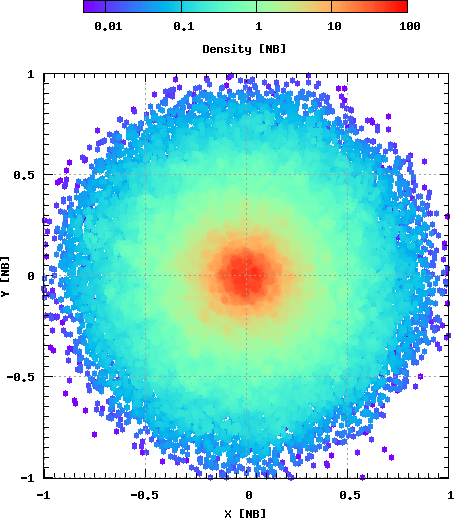
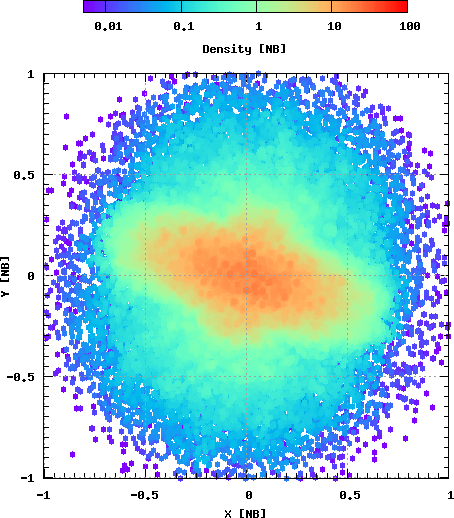
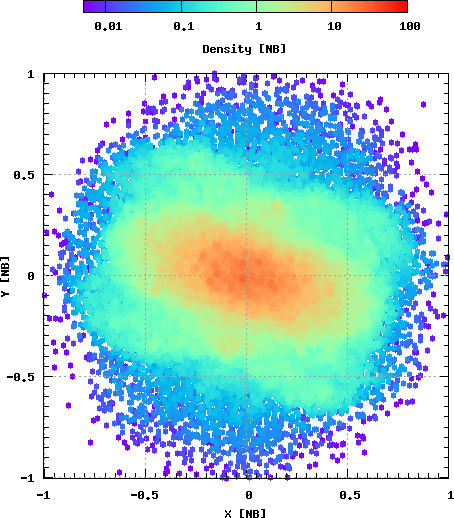
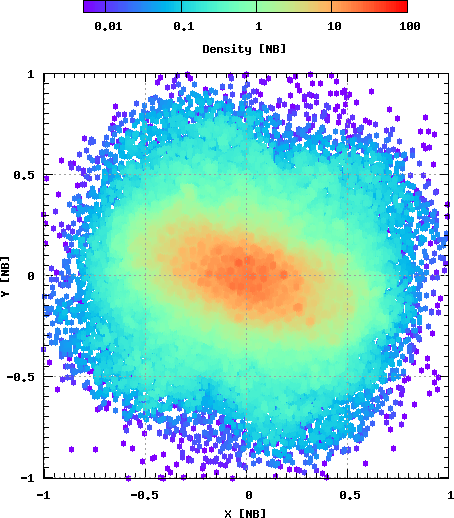
На Рис. 12 показан пример действия неустойчивости радиальных орбит: скопление из сферически-симметричного превращается в сплюнутую фигуру.