4.5 Устойчивость анизотропной сферы

В отличие от изотропных сфер, которые можно считать всегда устойчивыми (с некоторыми оговорками), анизотропные сферические системы могут быть неустойчивыми. Основной неустойчивость в такой системе является неустойчивость радиальных орбит. Кроме того, может иметь место гравитационная конусная неустойчивость, аналогичная конусной неустойчивости в плазменных магнитных ловушках.

4.5.1 Неустойчивость радиальных орбит

Впервые неустойчивость радиальных орбит была упомянута в работе В.Л. Поляченко и И.Г. Шухмана (1972) как аналог джинсовской неустойчивости по углу в анизотропной звездной системе. Они указали на то, что дисперсия в радиальном направлении в системах с орбитами, близкими к радиальным, всегда большая и порядка (оценка использует вириальные скорости)

где $M$ и $R$ – масса и радиус системы, ${\Omega }_{\mathrm{\text{J}}}$ – джинсовская частота. Отсюда получаем оценку на характерный джинсовский масштаб

Т.е. мы получили, что джинсовский масштаб порядка радиуса системы. Если бы он оказался существенно меньше $R$, то можно было бы ожидать джинсовской неустойчивости по радиусу, но подробные исследования показали, что такой неустойчивости не существует даже для модели с почти круговыми орбитами, в которых радиальная дисперсия мала [А.Б. Михайловский, А.М. Фридман, Я. Эппельбаум, 1971].

В отличие от радиального направления, в направлении поперек радиуса возможна сколь угодно малая дисперсия скоростей. Это позволяет надеятся, что по крайней мере для почти радиальных орбит такая неустойчивость может иметь место. Первое доказательство существования неустойчивости радиальных орбит было дано Антоновым в 1973 г., но оно содержало некорректность из-за наличия в доказательстве расходящихся интегралов [Поляченко Е.В. и Шухман И.Г., Письма в Астрон. Журн., 42, 120 (2016)]. Другая интерпретация неустойчивости основана на введении понятия прецессирующих симметричных звездных орбит, способных притягиваться и создавать неустойчивость [Lynden-Bell, MNRAS, 187, 101 (1979)]. Численное доказательство впервые было проведено Поляченко В.Л. [Письма в Астрон. Журн., 7, 142 (1981)].

Численные исследования включали в себя не только решение задачи $N$ тел, но и использование матричного метода для сфер [Поляченко В.Л. и Шухман И.Г. Астрон. журн. 58, 933 (1981)].

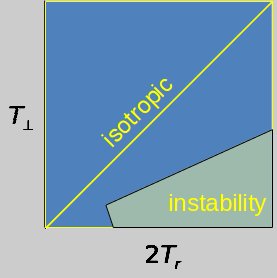
В первых численных работах были предприняты попытки установить критерий устойчивости в терминах глобальных характеристик системы – отношения энергий радиального и трансверсального движений $\zeta =\frac{2T_r}{T_{\perp }}$. Найденный на примере моделей Идлиса диапазон $\zeta =1.75\pm 0.25$ оказался не универсальным, а в значительной степени зависящим от модели и позднее был расширен вплоть до изотропных моделей.

Рис. 7: Первые представления об устойчивых и неустойчивых областях различных фазовых моделей в терминах отношения энергий радиального и трансверсального движений.

4.5.2 Гравитационная конусная неустойчивость

В магнитных ловушках плазма удерживается сильным магнитным полем (Рис. 8).

Рис. 8: Магнитная ловушка, образованная сильным продольным магнитным полем.

Однако в направлении вдоль поля плазма может уходить и из-за этого возникает провал ФР по поперечным скоростям. Оказывается, такой провал инициирует конусную неустойчивость, которая изменяет ФР, в результате чего вся плазма быстро вытекает через кунус потерь.

Рис. 9: ФР с конусом потерь и ее изменение благодаря действию конусной неустойчивости.

Рис. 10: Образование конуса потерь вблизи черной дыры из-за захвата звезд или приливного разрушения.

Аналогичная ситуация может быть и в гравитирующих системах, что первоначальный конус потерь создается разрушением или поглощением звезд черной дырой. Насколько глубоким должен быть конус потерь, какой вид функции распределения и как сказывается геометрия на возникновение этой новой неустойчивости? Оказывается, что такая неустойчивость может иметь место только в системах с обратной прецессией, как например в звездных скоплениях в поле массивной черной дыры. При этом неустойчивость проявляется только для сферических гармоник с $l\ge 3$.